You are here
Stochastic Physics
Instead of explicitly resolving small-scale processes by increasing the resolu;on of climate models, a computationally cheaper alternative is to use stochastic parameterization schemes. A stochastic scheme includes a statistical representaJon of the small scales, and hence is able to represent the impact of such small-scale processes on the resolved scale. Practically, there are Gaussian perturbations applied on the 3D field tendencies. There is mounting evidence that stochastic parameterizations are beneficial for climate variability in GCM simulations (Dawson et al, 2012).
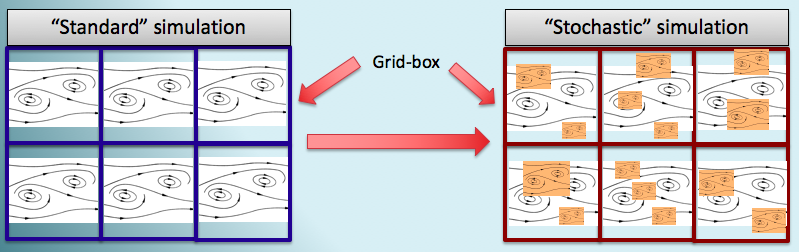
The motivation for including stochastic approaches in our current generation of weather and climate models is two-fold, and is clearly set out in a recent essay by Palmer (2012). Firstly, deterministic parameterisations in sophisticated weather and climate models are inconsistent with the implications of the scaling symmetries in the Navier-Stokes equations, and with the observed power-law behaviour in the atmosphere. This prevents a meaningful separation between resolved and unresolved scales, as is assumed possible in deterministic parameterisation. One important consequence of the power-law structure in the atmosphere is the upscale propagation of errors, whereby errors at very small scales (only resolved in high horizontal resolution models) can grow and ultimately contaminate the accuracy of larger scales in a finite time. A stochastic scheme includes a statistical representation of the small scales, so it is able to represent this process. The second motivation for stochastic parameterisations is that they provide a skilful estimate of model uncertainty due to truncation of the model equations, which is necessary for producing reliable forecasts (Berner et al, 2009; Weisheimer et al, 2011).
There is mounting evidence that stochastic parameterisations prove beneficial for climate simulations (e.g., Lin and Neelin 2000, 2003; Arnold et al. 2013). In two recent papers (Weisheimer et al. 2014, Dawson and Palmer 2014) it has been indeed demonstrated that the simulation of regimes can be significantly improved, even at modest model resolution, by the introduction of a stochastic physics scheme. These results highlight the importance of small-scale processes on large-scale climate variability, and indicate that although simulating variability at small scales is a necessity, it may not be necessary to represent the small-scales accurately, or even explicitly, in order to improve the simulation of large-scale climate.








